【簡単エクセル/Excel】標準偏差（σ）を求める方法｜STDEV.S/STDEV.P｜Excel関数（エクセル関数） #003

いつもありがとうございます。

「わかりやすいExcel関数解説シリーズ」へようこそ。

本稿では、「Excelで標準偏差を求める方法」を、わかりやすく解説いたします。

統計データを扱う際、データの散らばり具合や分布の形状を把握するために「標準偏差」は欠かせない指標です。Excelには、この標準偏差を手軽に計算できる関数が用意されています。本記事では、データが平均値からどれくらい離れているかを示す標準偏差の基本概念と、Excelでの関数の使い方をわかりやすく解説します。

Excel関数で自分に合ったデータを作成し、仕事量は半分に、成果は2倍にしていきましょう。

初心者でも理解しやすいように、分かりやすく解説していきます。ぜひご覧ください。

標準偏差とは？

「標準偏差」とは、データが平均値からどれだけ離れているかを示す指標であり、データの散らばり具合を定量的に表します。これは統計分析において重要な役割を果たし、データ全体の分布を理解するうえで非常に有用です。

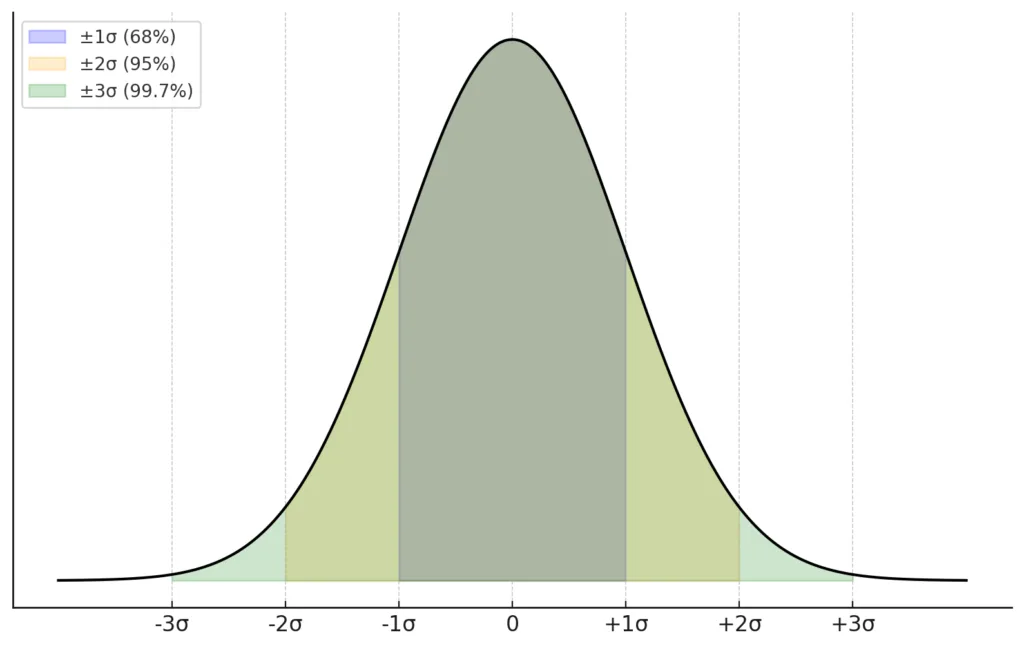
特にデータが正規分布に従う場合、標準偏差の意味が一層明確になります。正規分布とは、データが平均値を中心に左右対称に広がる鐘形の分布で、多くの自然現象や測定結果がこの分布に近い傾向を示します。

正規分布において、標準偏差（σ）を基準にデータがどの範囲に収まるかを考えることがよくあります。具体的には、平均値から±1σの範囲に全データの約68％が、±2σの範囲に約95％、±3σの範囲に約99.7％が収まります。この特性を利用することで、データが期待される範囲内に分布しているか、異常値や外れ値が存在するかを容易に判断できます。

このように、標準偏差は品質管理やリスク評価などの分野で頻繁に活用され、データのばらつきを評価するための重要な指標となっています。

Excelで標準偏差を求める方法

次に示すデータは、ある部品の寸法を測定した結果です。このデータをもとに、標準偏差を求めてみましょう。

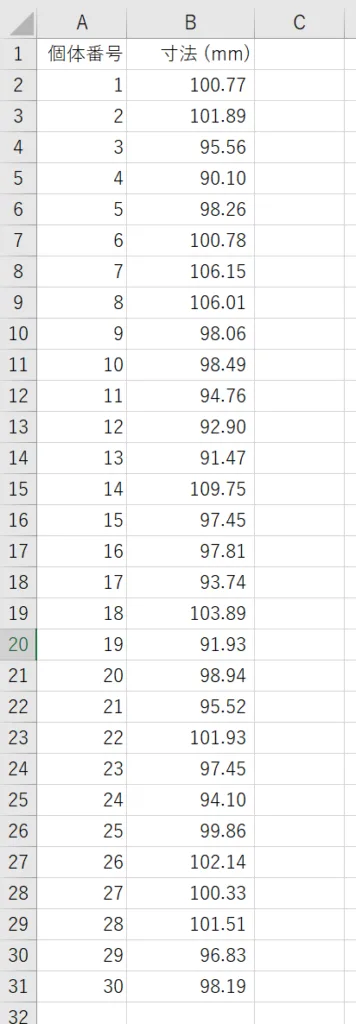
寸法データの下部に次の数式を設定します。なお、データ数が多いため、下図では一部のデータを省略して表示しています。

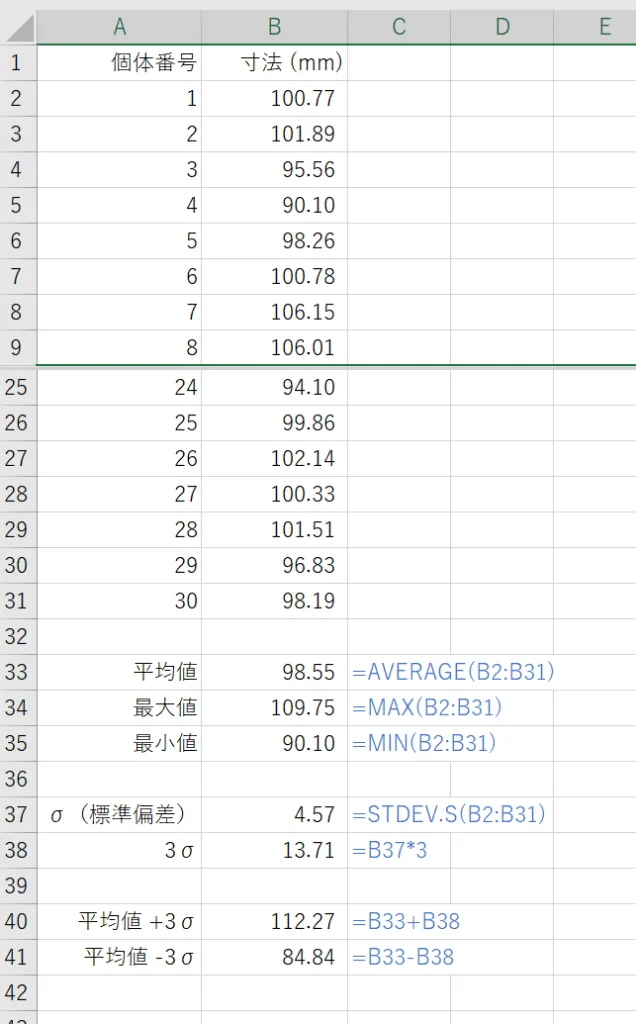
解説します。

まず、このシート下部の基本的な見方を説明します。A列に示した項目に対応する数式がB列に入力されています。C列には、どのような関数が使われているかを分かりやすく示すために、関数を青字で表示しています。関数の括弧内に表示されている「B2:B31」は、関数を使って計算する対象のデータの範囲を表します。

このシートでは、まず平均値、最大値、最小値を設定しています。これら3つの指標は、データの基本的な傾向を把握するために、どのような分析でも欠かせない重要な項目です。

次に、σ（標準偏差）と3σの数式を設定しています。σは「シグマ」と呼ばれ、標準偏差を表す記号です。3σはその3倍の値を意味します。

最後に、平均値+3σと平均値-3σの数式を設定しています。この±3σの範囲にデータの約99.7％が収まる、ということです。

それでは、最大値、最小値、平均値、標準偏差を求める各関数の構文を確認してみましょう。各関数の構文は次に示す通りです。「＝」記号に「各関数を表す単語」をつなげ、さらにその後に「括弧」をつなげ、その括弧の中に「データ範囲」を入力する構文になっています。

' 最大値
=MAX(データ範囲)

' 最小値
=MIN(データ範囲)

' 平均値
=AVERAGE(データ範囲)

' 標準偏差（標本）
=STDEV.S(データ範囲)

' 標準偏差（母集団）
=STDEV.P(データ範囲)

この構文に示した通り、標準偏差には2つの計算方法があります。それぞれの意味は下表の通りです。

なお、今回の例では、30台の寸法データが標本であると仮定して計算しています。実際の分析の現場では、すべてのデータ（母集団全体）が揃うことはまれだと思いますので、STDEV.S が使われることが多いと思います。

以上で、解説は終了です。ありがとうございました。

おわりに

ご覧いただきありがとうございました。

本稿では、「Excelで標準偏差を求める方法」を解説いたしました。

お問い合わせやご要望等ございましたら、「お問い合わせ／ご要望」またはコメントにて、ご連絡いただければ幸いでございます。

皆様の人生がより一層素晴らしいものになるよう、少しでもお役に立てれば幸いでございます。

なお、当サイトでは様々な情報を発信しております。もしよろしければ、トップページもご覧いただけると幸いでございます。

• トップページ

Excel関数スキルアップのための参考情報

Excel関数に関する書籍は数多く出版されています。もし興味がございましたら、チェックしてみてください。入門書に関しては、どの書籍も大きな違いはありません。あまり悩むことに時間をかけるよりは、手頃なものを一冊選んでみると良いでしょう。